Desde los latidos del corazón hasta el diseño de rascacielos: descubre cómo el movimiento periódico y la resonancia controlan el ritmo y el equilibrio del cosmos.
Desde la vibración de un cristal de cuarzo en un reloj hasta el movimiento rítmico de los pistones de un motor, el universo parece estar tocando una melodía mecánica. Este fenómeno, conocido como movimiento u oscilación periódicos, no es simplemente una curiosidad científica; es el lenguaje básico que nos ayuda a captar las ondas, el sonido, la luz e incluso la corriente alterna que alimenta nuestros hogares. Fundamentalmente, se trata de un sistema que busca ansiosamente su centro, un punto de equilibrio estable que, cuando se altera, es empujado hacia atrás por una fuerza restauradora. Sin embargo, la inercia lo obliga a ir más allá de ese centro, creando un ciclo de movimiento que da forma a la esencia misma del tiempo.
El alfabeto de la oscilación
Para hablar de las oscilaciones, primero debemos entender sus conceptos clave. La amplitud (A) indica el punto más alto de desplazamiento desde el centro, lo que significa la “fuerza” de la vibración. El período (T) mide la duración hasta terminar un ciclo completo, mientras que la frecuencia (f) muestra cuántos ciclos ocurren en un segundo, expresado en hercios (Hz).
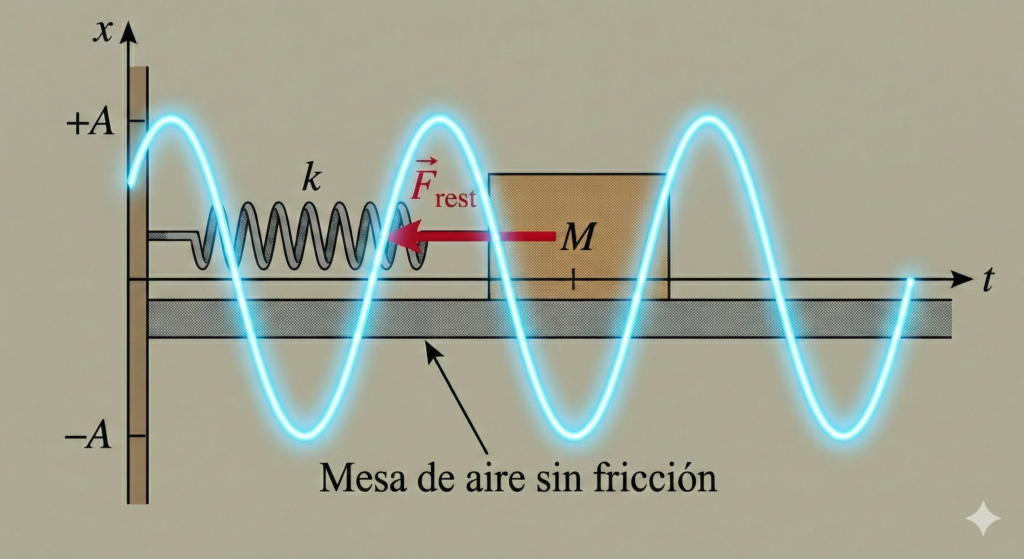
Hay una idea más refinada: la frecuencia angular (ω). Esto vincula la oscilación lineal con la suavidad del movimiento circular, recordándonos que cada movimiento es, de hecho, la sombra de una rotación constante sobre un diámetro. Como señala Hernández (2024), “el equilibrio de un sistema biológico o mecánico depende de la precisión de estos factores, donde la armonía es esencial para la estabilidad estructural”.
Movimiento Armónico Simple: el modelo ideal
El movimiento Armónico Simple (MAS) es el punto de referencia para las oscilaciones. Ocurre cuando la fuerza restauradora está directamente relacionada con el desplazamiento, de acuerdo con la conocida Ley de Hooke (Fx = -kx). En esta situación perfecta, ocurre algo interesante: el período de oscilación no se ve afectado por la amplitud. Esto indica que, independientemente de que un diapasón vibre con mucha fuerza o solo un poco, su nota musical, o frecuencia, permanece igual, lo que nos permite afinar los instrumentos con cálculos exactos.
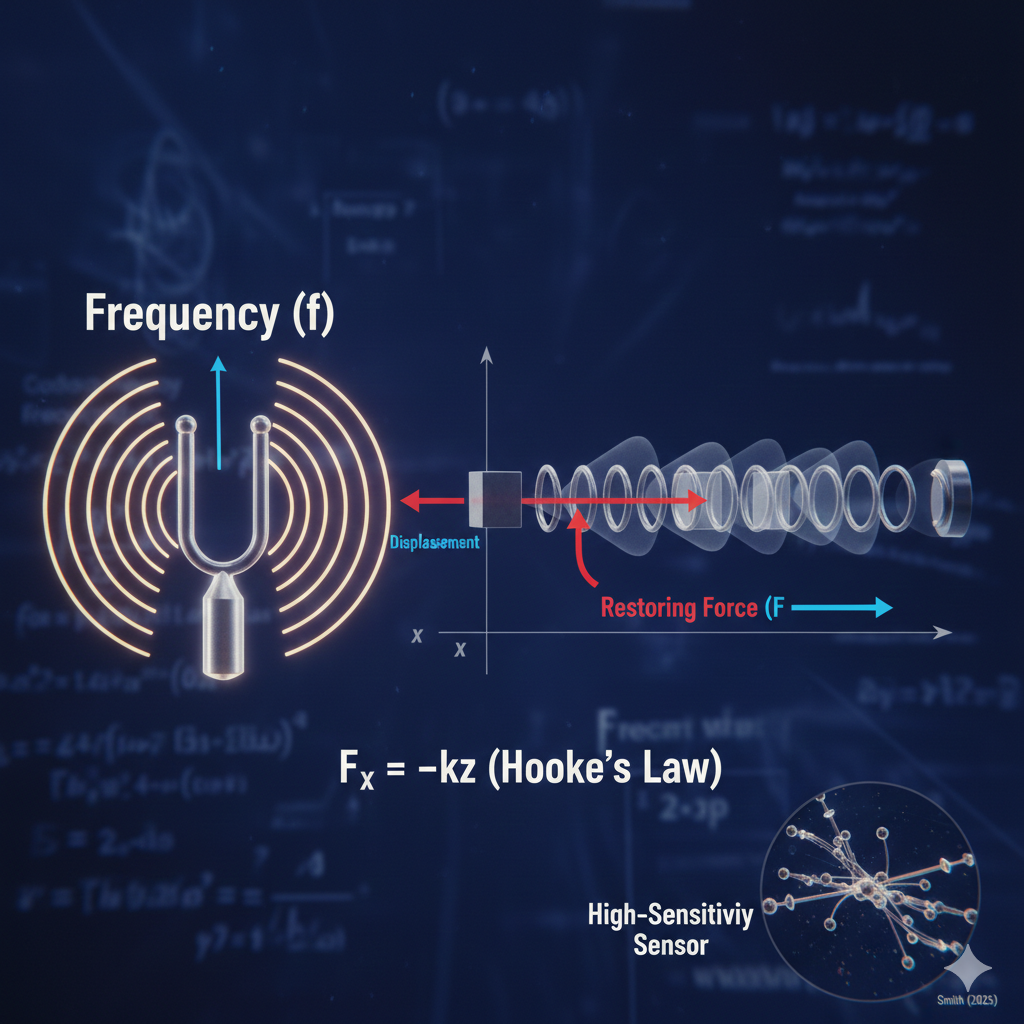
Los hallazgos recientes en materiales inteligentes comprueban que esta linealidad es fundamental para crear sensores de alta sensibilidad. Como afirma Smith (2025), “el ajuste de la constante de fuerza en los microosciladores permite detectar cambios masivos a nivel molecular, lo que allana el camino para un diagnóstico médico inmediato” (p. 42).
El intercambio eterno: energía en el MAS
En un sistema ideal sin fricción, la energía se comporta como una moneda de cambio constante. En los puntos de máximo desplazamiento, la energía es puramente potencial ((1/2) k A2), quedando almacenada por completo en la deformación del resorte. A medida que se mueve por el punto de equilibrio, se transforma por completo en energía cinética ((1/2)m vmax2). La suma de ambas formas es la energía mecánica general (E), que permanece constante y depende únicamente de la rigidez del sistema y del cuadrado de su amplitud.
E = (1/2)m vx2 + (1/2)kx2 = (1/2) k A2

Este equilibrio es fundamental para el diseño de bioprótesis. Kim (2026) señala que “los modelos de biofísica cardiovascular utilizan el MAS para reproducir la flexibilidad de las válvulas cardíacas, donde preservar la energía mecánica es esencial para reducir el deterioro de los tejidos” (p. 112).
Historia y naturaleza del conocimiento oscilatorio
La comprensión del movimiento periódico pasó de una observación cuidadosa a una ingeniería exacta. Al observar una lámpara oscilante en la catedral de Pisa, Galileo Galilei se dio cuenta de la isocronicidad del péndulo: el concepto de que el tiempo de oscilación no depende del tamaño de la oscilación. Más tarde, Robert Hooke estableció la conexión entre fuerza y elasticidad, mientras que Heinrich Hertz nombró a la unidad de frecuencia al estudiar las ondas electromagnéticas.
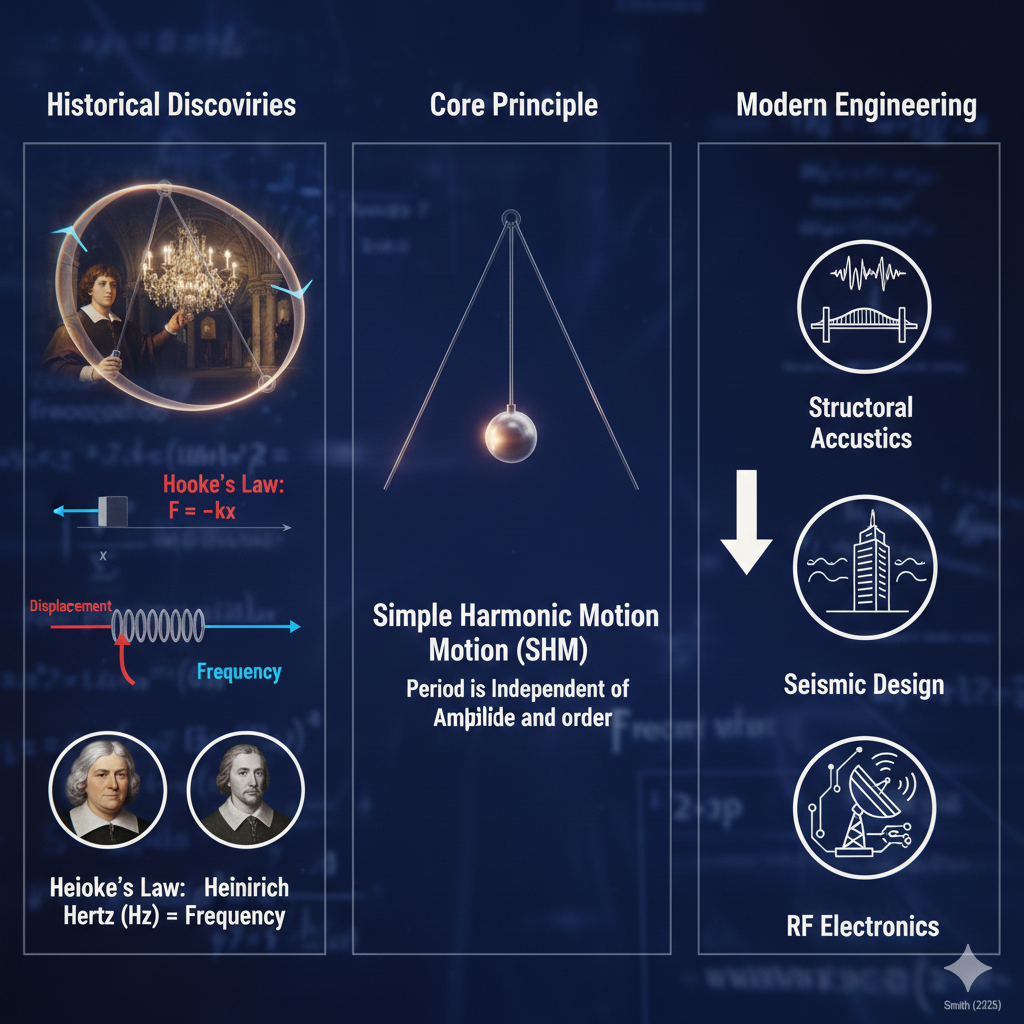
Este conocimiento no es simplemente una colección de hechos, sino un cambio significativo en la forma de pensar: reveló que la naturaleza favorece la estabilidad y que el orden puede surgir de la repetición. Se enseña en ciencia e ingeniería porque constituye la base de los sistemas más intrincados: sin comprender el MAS, no se puede entender la acústica estructural, el diseño sísmico o la electrónica de radiofrecuencia.
Evidencia cotidiana: el mundo en vibración
Las oscilaciones están presentes en nuestra vida diaria, desde la música que escuchamos hasta la tecnología que utilizamos, subrayando la importancia del movimiento periódico en diversas aplicaciones.
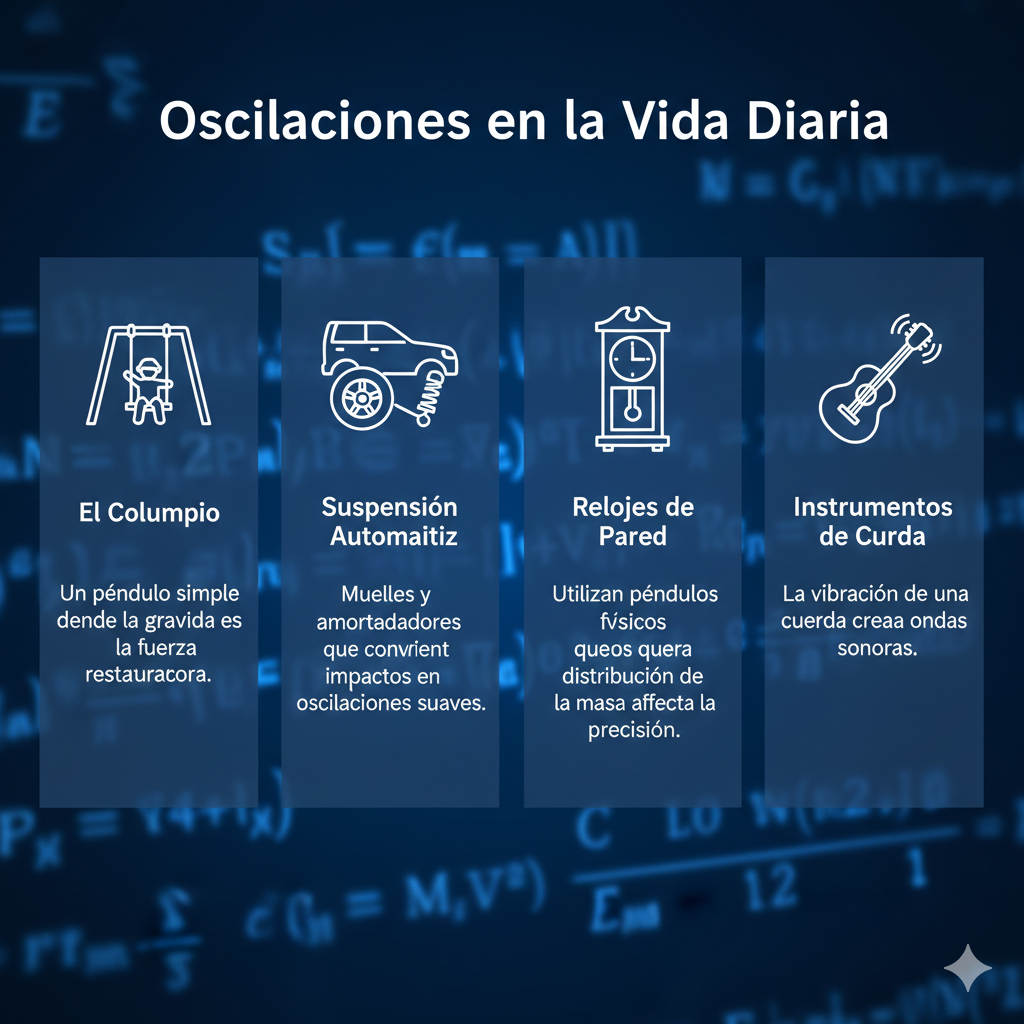
A continuación algunas de estas:
- The Swing: Un ejemplo sencillo de un péndulo simple en el que la gravedad actúa como fuerza restauradora.
- Suspensión automotriz: Los muelles y los amortiguadores de un automóvil funcionan para amortiguar los impactos, convirtiendo un golpe repentino en una oscilación suave.
- Relojes de pared: utilizan péndulos físicos en los que la distribución de la masa afecta a la precisión de cada segundo.
- Instrumentos de cuerda: La vibración de una cuerda de guitarra forma un sistema oscilante que envía energía al aire en forma de ondas sonoras.
Aplicaciones en la ingeniería y las ciencias
El movimiento periódico y la resonancia son fundamentales en la ingeniería, permitiendo el diseño de estructuras más seguras y eficientes, así como el desarrollo de tecnologías innovadoras en diversos campos.
Por ejemplo:
- Ingeniería mecánica y civil: los rascacielos utilizan “amortiguadores de masa ajustados” para el diseño sísmico. Rodríguez (2024) afirma que estos sistemas reducen la energía sísmica mediante oscilaciones amortiguadas, lo que evita las fallas estructurales.
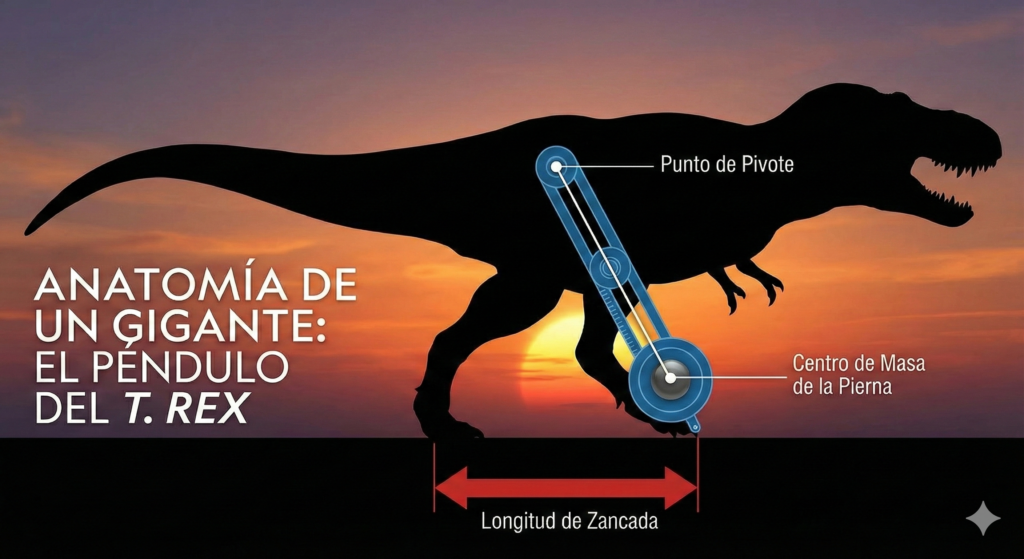
- Mecatrónica y robótica: el análisis de la marcha, incluso en el caso de dinosaurios como el T. rex, se modela con péndulos físicos para estudiar la eficiencia energética del movimiento.
- Biotecnología y medicina: el diseño de los transductores ultrasónicos para el diagnóstico médico se basa en oscilaciones de frecuencia extremadamente altas (millones de ciclos por segundo).
- Química molecular: las moléculas de gas, como el argón, vibran como si estuvieran conectadas por resortes invisibles; conocer estas frecuencias permite identificar las sustancias mediante espectroscopía.
Oscilaciones amortiguadas y el fenómeno de resonancia
En el mundo real, la energía se pierde debido a la fricción o la resistencia del aire, lo que se conoce como amortiguamiento. Sin una fuerza externa, la amplitud cae rápidamente hasta que se detiene. Sin embargo, al aplicar una fuerza impulsora periódica, podemos mantener el movimiento. Aquí se produce la resonancia: cuando la frecuencia de la fuerza externa se alinea con la frecuencia natural del sistema, la amplitud aumenta significativamente. Esto puede ser hermoso, como en la caja de resonancia de un violín, o desastroso, como el derrumbe del puente Tacoma Narrows, donde el viento «alimentó» las oscilaciones hasta romper el acero.

El movimiento periódico es el pulso invisible de la realidad. Desde partículas diminutas hasta estructuras masivas, todo oscila, vibra y resuena. Comprender estos principios no es solo un esfuerzo académico; se trata de aprender a conectarse con el ritmo del universo. Te animo a observar: cada swing ofrece una lección de física lista para ser entendida.
Autor: Oscar E. Hernández B.